Question

Suposse that test scores are normally distributed with an unknown mean and standard deviation. The scores of 20 students are used to estimate the mean score. What t-score should be used to find the 90% confidence interval for the Suppose that test scores are population mean score?

df to.10 to.05 to.025 to.01 to.005
19 1.328 1.729 2.093 2.539 2.861
20 1.325 1.725 2.086 2.528 2.845
21 1.323 1.721 2.080 2.518 2.831
22 1.321 1.717 2.074 2.508 2.819

Answer 1

The t-score that should be used to find the 90% confidence interval is 1.729.

Explanation:

The (1 - α)% confidence interval population mean, when the population standard deviation is not known is:

`CI=\bar x\pm t_(\alpha/2, (n-1))\cdot (s)/(√(n))`

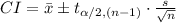
The information provided is:

n = 20

α = 0.10

The degrees of freedom of t-statistic will be:

df = n - 1

= 20 - 1

= 19

Compute the critical value of t as follows:

`t_(\alpha/2, (n-1))=t_(0.10/2, 19)=1.729`

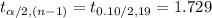
*Use a t-table.

Thus, the t-score that should be used to find the 90% confidence interval is 1.729.