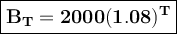Question

The balance of an investment is increasing according to the rule: Next year’s balance = 1.08 x current balance What is the constant percent increase per year? If the original balance of the investment was $2000 find a formula that gives the balance B (in dollars) after T years.

Answer 1

`\large \boxed{1. 8 \, \%; \, 2. \, B_(T) = 2000(1.08)^(T)}`

Explanation:

1. Rate of increase

Let B = this year's balance. Then

1.08B = next year's balance

1.08B = B + 0.08B = B + 8 % of B

`\text{The rate of increase of B is $\large \boxed{\mathbf{8 \%}}$ per year.}`

2. The formula

Each year, the balance is multiplied by 1.08.

The end of a year is the same as the end of the previous year.

If T = the number of years, then the balance at the beginning of Year 1 is B₀.

`B_(T) = B_(0)(1.08)^(T)`

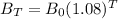
If B₀ = $2000, the formula becomes

`\large \boxed{\mathbf{B_(T) = 2000(1.08)^(T)}}$`

Answer 2

The constant percent increase per year is 8%.

In which B(0) is the initial amount and r is the growth rate, as a decimal.

Next year’s balance = 1.08 x current balance

So

`B(1) = (1.08)B(0)`

This means that:

`1 + r = 1.08`

`r = 1.08 - 1`

`r = 0.08`

The constant percent increase per year is 8%

If the original balance of the investment was $2000 find a formula that gives the balance B (in dollars) after T years.

This means that
`B(0) = 2000`

So

`B(T) = B(0)(1+r)^(T)`

`B(T) = 2000(1+0.08)^(T)`

[tex]B(T) = 2000(1.08)^{T}{/tex]