Question

A computer consulting firm presently has bids out on three projects. Let Ai = {awarded project i}. for i=1, 2, 3, and suppose that P(A1)=.22, P(A2)=.25, P(A3)=.28, P(A1 and A2)=.11, P(A1andA3)=.05, P(A2 and A3)=.07, P(A1 and A2 and A3)=.01. Compute the probability of each event: a) A 1or A2 b) A1c and A2c c) A1 or A2 or A3 d) A1c and A2c and A3c e) A1c and A2c and A3 f) (A1c and A2c) or A3

Answer 1

(a) 0.36

(b) 0.64

(c) 0.53

(d) 0.47

(e) 0.17

(f) 0.77

Explanation:

(a)

Compute the value of P (A₁ ∪ A₂) as follows:

`P(A_(1)\cup A_(2))=P(A_(1))+P(A_(2))-P(A_(1)\cap A_(2))`

`=0.22+0.25-0.11\\=0.36`

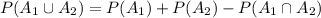
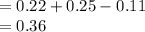
Thus, the value of P (A₁ ∪ A₂) is 0.36.

(b)

Compute the value of P (A₁' ∩ A₂') as follows:

`P(A'_(1)\cap A'_(2))=1-P(A_(1)\cup A_(2))`

`=1-0.36\\=0.64`

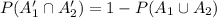
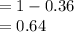
Thus, the value of P (A₁' ∩ A₂') is 0.64.

(c)

Compute the value of P (A₁ ∪ A₂ ∪ A₃) as follows:

`P(A_(1)\cup A_(2)\cup A_(3))=P(A_(1))+P(A_(2))+P(A_(3))-P(A_(1)\cap A_(2))-P(A_(2)\cap A_(3))-P(A_(1)\cap A_(3))+P(A_(1)\cap A_(2)\cap A_(3))`

`=0.22+0.25+0.28-0.11-0.05-0.07+0.01\\=0.53`

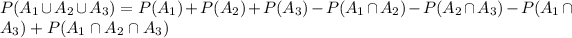
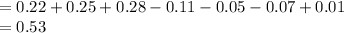
Thus, the value of P (A₁ ∪ A₂ ∪ A₃) is 0.53.

(d)

Compute the value of P (A₁' ∩ A₂' ∩ A'₃) as follows:

`P(A'_(1)\cap A'_(2)\cap A'_(3))=1-P(A_(1)\cup A_(2)\cup A_(3))`

`=1-0.53\\=0.47`

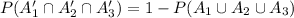
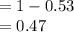
Thus, the value of P (A₁' ∩ A₂' ∩ A'₃) is 0.47.

(e)

Compute the value of P (A₁' ∩ A₂' ∩ A₃) as follows:

`P(A'_(1)\cap A'_(2)\cap A_(3))=P(A_(3))-[P(A_(1)\cap A_(3))+P(A_(2)\cap A_(3))-P(A_(1)\cap A_(2)\cap A_(3))]`

`=0.28-(0.05+0.07-0.01)\\=0.28-0.11\\=0.17`

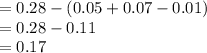
Thus, the value of P (A₁' ∩ A₂' ∩ A₃) is 0.17.

(f)

Compute the value of P ((A₁' ∩ A₂') ∪ A₃) as follows:

`P((A'_(1)\cap A'_(2))\cup A_(3))=P(A'_(1)\cup A'_(2)\cup A'_(3))+P(A_(3))`

`=0.49+0.28\\=0.77`

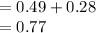
Thus, the value of P ((A₁' ∩ A₂') ∪ A₃) is 0.77.