Question

g An irate student complained that the cost of textbooks was too high. He randomly surveyed 36 other students and found that the mean amount of money spent for textbooks was $121.60. If the standard deviation of the population was $6.36, find the 90% confidence interval of the true mean.

Answer 1

A 90% confidence interval of the true mean is [$119.86, $123.34].

Explanation:

We are given that an irate student complained that the cost of textbooks was too high. He randomly surveyed 36 other students and found that the mean amount of money spent on textbooks was $121.60.

Also, the standard deviation of the population was $6.36.

Firstly, the pivotal quantity for finding the confidence interval for the population mean is given by;

P.Q. =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean amount of money spent on textbooks = $121.60

`\sigma` = population standard deviation = $6.36

n = sample of students = 36

`\mu` = population mean

Here for constructing a 90% confidence interval we have used One-sample z-test statistics as we know about population standard deviation.

So, 95% confidence interval for the population mean,
`\mu` is ;

P(-1.645 < N(0,1) < 1.645) = 0.90 {As the critical value of z at 5% level

of significance are -1.645 & 1.645}

P(-1.645 <
`(\bar X-\mu)/((\sigma)/(√(n) ) )` < 1.645) = 0.90

P(
`-1.645 * {(\sigma)/(√(n) ) }` <
`{\bar X-\mu}` <
`1.645 * {(\sigma)/(√(n) ) }` ) = 0.90

P(
`\bar X-1.645 * {(\sigma)/(√(n) ) }` <
`\mu` <
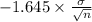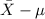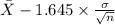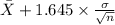`\bar X+1.645 * {(\sigma)/(√(n) ) }` ) = 0.90

90% confidence interval for
`\mu` = [
`\bar X-1.645 * {(\sigma)/(√(n) ) }` ,
`\bar X+1.645 * {(\sigma)/(√(n) ) }` ]

= [
`121.60-1.645 * {(6.36)/(√(36) ) }` ,
`121.60+1.645 * {(6.36)/(√(36) ) }` ]

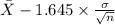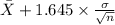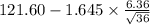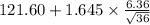= [$119.86, $123.34]

Therefore, a 90% confidence interval of the true mean is [$119.86, $123.34].