Question

According to a recent study, 1 in every 10 women has been a victim of domestic abuse at some point in her life. Suppose we have randomly and independently sampled twenty-five women and asked each whether she has been a victim of domestic abuse at some point in her life. Find the probability that more than 22 of the women sampled have not been the victim of domestic abuse

Answer 1

The probability that more than 22 of the women sampled have not been the victim of domestic abuse is P=0.537.

Explanation:

This problem can be modeled by a binomial random variable.

The probability p can be calculated as the proportion of women that has not been a victim of domestic abuse at some point in her life:

`p=1-(X)/(n)=1-(1)/(10)=1-0.1=0.9`

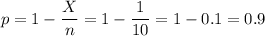
The sample size is n=25.

We want to calculate the probability that more than 22 of the women of the sample have not been victim of domestic abuse.

The probability that exactly k women have not been victim of domestic abuse can be calculated as:

`P(x=k) = \dbinom{n}{k} p^(k)(1-p)^(n-k)\\\\\\P(x=k) = \dbinom{25}{k} 0.9^(k) 0.1^(25-k)\\\\\\`

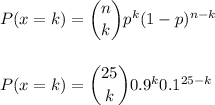
Then, the probability that more than 22 of the women sampled have not been the victim of domestic abuse is:

`P(x>22)=P(x=23)+P(x=24)+P(x=25)\\\\\\P(x=23) = \dbinom{25}{23} p^(23)(1-p)^(2)=300*0.089*0.01=0.266\\\\\\P(x=24) = \dbinom{25}{24} p^(24)(1-p)^(1)=25*0.08*0.1=0.199\\\\\\P(x=25) = \dbinom{25}{25} p^(25)(1-p)^(0)=1*0.072*1=0.072\\\\\\\\P(x>22)=0.266+0.199+0.072=0.537`