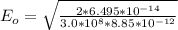Question

Reception devices pick up the variation in the electric field vector of the electromagnetic wave sent out by the satellite. Given the satellite specifications listed in the problem introduction, what is the amplitude E0 of the electric field vector of the satellite broadcast as measured at the surface of the earth? Use ϵ0=8.85×10−12C/(V⋅m) for the permittivity of space and c=3.00×108m/s for the speed of light.

Answer 1

The amplitude of the electric field is determined as 9 x 10¹⁶ V/m.

How to calculate the amplitude of the electric field?

The amplitude of the electric field is calculated by applying the following formula as shown below;

E₀ = c / √ (μ₀ε₀)

where;

• c is speed of light
• μ₀ is permeability of free space
• ε₀ is permittivity of free space

The amplitude of the electric field is calculated as follows;

E₀ = (3 x 10⁸) / √ (4π x 10⁻⁷ x 8.85 x 10⁻¹²)

E₀ = 9 x 10¹⁶ V/m

Thus, the amplitude of the electric field is determined as 9 x 10¹⁶ V/m.

Answer 2

Complete Question

A satellite in geostationary orbit is used to transmit data via electromagnetic radiation. The satellite is at a height of 35,000 km above the surface of the earth, and we assume it has an isotropic power output of 1 kW (although, in practice, satellite antennas transmit signals that are less powerful but more directional).

Reception devices pick up the variation in the electric field vector of the electromagnetic wave sent out by the satellite. Given the satellite specifications listed in the problem introduction, what is the amplitude E0 of the electric field vector of the satellite broadcast as measured at the surface of the earth? Use ϵ0=8.85×10^−12C/(V⋅m) for the permittivity of space and c=3.00×10^8m/s for the speed of light.

Answer:

The electric field vector of the satellite broadcast as measured at the surface of the earth is
`E_o = 6.995 *10^(-6) \ V/m`

Step-by-step explanation:

From the question we are told that

The height of the satellite is
`r = 35000 \ km = 3.5*10^(7) \ m`

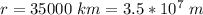
The power output of the satellite is
`P = 1 \ KW = 1000 \ W`

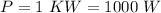
Generally the intensity of the electromagnetic radiation of the satellite at the surface of the earth is mathematically represented as

`I = (P)/(4 \pi r^2)`

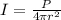
substituting values

`I = (1000)/(4 * 3.142 (3.5*10^(7))^2)`

`I = 6.495*10^(-14) \ W/m^2`

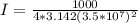
This intensity of the electromagnetic radiation of the satellite at the surface of the earth can also be mathematically represented as

`I = c * \epsilon_o * E_o^2`

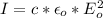
Where
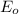`E_o` is the amplitude of the electric field vector of the satellite broadcast so

`E_o = \sqrt{(2 * I)/(c * \epsilon _o) }`

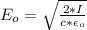
substituting values

`E_o = \sqrt{(2 * 6.495 *10^(-14))/(3.0 *10^(8) * 8.85*10^(-12)) }`

`E_o = 6.995 *10^(-6) \ V/m`