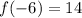What does the remainder theorem conclude given that (f(x))/(x+6) has a remainder of 14? f(?) = ? Please help this is literally all the information I was given and I've trie…

Question

What does the remainder theorem conclude given that
`(f(x))/(x+6)` has a remainder of 14? f(?) = ? Please help this is literally all the information I was given and I've tried to figure it out so many different ways and it's just not working.

Answer 1

`f(-6)=14`

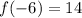
Explanation:

The remainder theorem tells us that If a polynomial f(x) is divided by a linear factor, L(x)=x-a, the remainder of the quotient is f(a).

In this case:

f(x) divided by x+6 has a remainder of 14.

• The Polynomial =f(x)
• Linear Factor = x+6

Comparing the linear factor with x-a, we have:

`x+6=x-(-6)`

Therefore the remainder of the quotient:

`f(-6)=14`