Question

Given:

MNOP is a parallelogram
Prove:
PM  ON
(For this proof, use only the definition of a parallelogram; don’t use any properties)

Answer 1

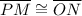`\overline{PM}\cong\overline{ON}`:, Segment subtended by the same angle on two adjacent parallel lines are congruent

Explanation:

Statement, Reason

MNOP is a parallelogram:, Given

`\overline{PM}\left | \right |\overline{ON}`:, Opposite sides of a parallelogram

∠PMO ≅ ∠MON:, Alternate Int. ∠s Thm.

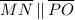`\overline{MN}\left | \right |\overline{PO}`:, Opposite sides of a parallelogram

∠POM ≅ ∠NMO:, Alternate Int. ∠s Thm.

OM ≅ OM:, Reflexive property

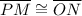`\overline{PM}\cong\overline{ON}`:, Segment subtended by the same angle and on two adjacent parallel lines are congruent