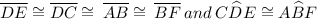Question

ABCD is a square. Two equilateral triangles AED and BFC have been constructed on the sides AD and BC respectively. Prove that triangle ABF is congruent to triangle CDE.

Answer 1

Check below please.

Explanation:

Hi,

Let's plot the figure, 1 square and 2 equilateral triangles.

1) Let's remember all the angles we already know, from the square and the equilateral triangle from their respective definition.

In other words:

Statement Reason

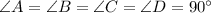`\angle A=\angle B=\angle C=\angle D=90^(\circ)` Given

`\bigtriangleup AED \cong \bigtriangleup BFC`
`\overline{AE}\cong \overline{AD}\cong \overline{ED} \:and\: A\widehat{E}D\cong A\widehat{D}E\cong D\widehat{A}E=60^(\circ)\\\overline{BF}\cong \overline{FC}\cong \overline{BC} \:and\: A\widehat{E}D\cong A\widehat{D}E\cong D\widehat{A}E=60^(\circ)\\`

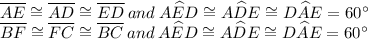
2) We have two triangles ABF and CDE

`\bigtriangleup ABF, \:and \bigtriangleup CDE \\A\widehat{B}F=C\widehat{D}E=90^(\circ)+60^(\circ)=150^(\circ)`

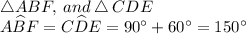
3) The Side, Angle Side Congruence Theorem assures us that both triangles are congruent. When there are two known legs (4 cm and 4 cm) of each triangle, and their respective formed angle is also known (150º). Therefore, these two triangles are both congruent.

Statement Reason

`\overline{DE}\cong \overline{DC} \cong\:\overline{AB}\cong \:\overline{BF} \:and \:C\widehat{D}E \cong A\widehat{B}F`
`SAS \:Theorem`