Question

Each letter in the expression shown to the right represents a digit other than zero. Different letters represent different digits and the same letter always represents the same digit. What is the smallest whole number that can be the value of this expression?

Answer 1

The smallest whole number that can be the value of the expression is 2

Explanation:

Given that the letters represent different digits, to get the smallest whole number value for the expression we have;

`(K * A * N * G * A * R * O * O)/(G * A * M * E)`

The letters G and A cancel out from the numerator and the denominator to give;

`(K * A * N * R * O * O)/(M * E)`

Therefore, the smallest whole number can be from 2 and above as the product of six digits is more than one times the product of two digits

If we put

K = 2, A = 3, N = 4, R = 6, O = 1, M = 9, and E = 8, we have;

`(2 * 3 * 4 * 6 * 1 * 1)/(9 * 8) = (144)/(72) =2`

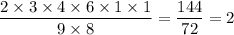
Therefore, the smallest whole number that can be the value of the expression = 2.