Question

A 2.45-kg frictionless block is attached to an ideal spring with force constant 355 N/m. Initially the spring is neither stretched nor compressed, but the block is moving in the negative direction at 11.0 m/s.

A. Find the amplitude of the motion.
B. Find the maximum acceleration of the block.
C. Find the maximum force the spring exerts on the block.

Answer 1

A. A = 0.913 m

B. amax = 132.24m/s^2

C. Fmax = 324.01N

Step-by-step explanation:

When the block is moving at the equilibrium point , its velocity is maximum.

A. To find the amplitude of the motion you use the following formula for the maximum velocity:

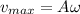`v_(max)=A\omega` (1)

vmax = maximum velocity = 11.0 m/s

A: amplitude of the motion = ?

w: angular frequency = ?

Then, you have to calculate the angular frequency of the motion, by using the following formula:

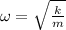`\omega=\sqrt{(k)/(m)}` (2)

k: spring constant = 355 N/m

m: mass of the object = 2.54 kg

`\omega = \sqrt{(355N/m)/(2.45kg)}=12.03(rad)/(s)`

Next, you solve the equation (1) for A and replace the values of vmax and w:

`A=(v)/(\omega)=(11.0m/s)/(12.03rad/s)=0.913m`

The amplitude of the motion is 0.913m

B. The maximum acceleration of the block is given by:

`a_(max)=A\omega^2 = (0.913m)(12.03rad/s)^2=132.24(m)/(s^2)`

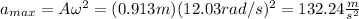
The maximum acceleration is 132.24 m/s^2

C. The maximum force is calculated by using the second Newton law and the maximum acceleration:

`F_(max)=ma_(max)=(2.45kg)(132.24m/s^2)=324.01N`

It is also possible to calculate the maximum force by using:

Fmax = k*A = (355N/m)(0.913m) = 324.01N

The maximum force exertedbu the spring on the object is 324.01 N