Question

20cm of 0.09M solution of H2SO4. requires 30cm of NaOH for complete neutralization. Calculate the

molar concentration of NaOH. (A) 0.12M (B) 0.0018M (C) 0.012M (D) 0.0036M
​

Answer 1

Choice A: approximately
`0.12\; \rm M`.

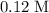Step-by-step explanation:

Note that the unit of concentration,
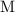`\rm M`, typically refers to moles per liter (that is:
`1\; \rm M = 1\; \rm mol\cdot L^(-1)`.)

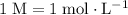On the other hand, the volume of the two solutions in this question are apparently given in
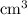`\rm cm^3`, which is the same as
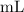`\rm mL` (that is:
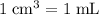`1\; \rm cm^(3) = 1\; \rm mL`.) Convert the unit of volume to liters:

• 
  `V(\mathrm{H_2SO_4}) = 20\; \rm cm^(3) = 20 * 10^(-3)\; \rm L = 0.02\; \rm L`.
• 
  `V(\mathrm{NaOH}) = 30\; \rm cm^(3) = 30 * 10^(-3)\; \rm L = 0.03\; \rm L`.

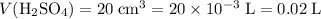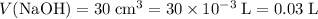Calculate the number of moles of
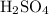`\rm H_2SO_4` formula units in that
`0.02\; \rm L` of the
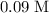`0.09\; \rm M` solution:

`\begin{aligned}n(\mathrm{H_2SO_4}) &= c(\mathrm{H_2SO_4}) \cdot V(\mathrm{H_2SO_4})\\ &= 0.02 \; \rm L * 0.09 \; \rm mol\cdot L^(-1) = 0.0018\; \rm mol \end{aligned}`.

Note that
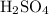`\rm H_2SO_4` (sulfuric acid) is a diprotic acid. When one mole of
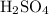`\rm H_2SO_4` completely dissolves in water, two moles of
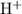`\rm H^(+)` ions will be released.

On the other hand,
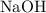`\rm NaOH` (sodium hydroxide) is a monoprotic base. When one mole of
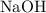`\rm NaOH` formula units completely dissolve in water, only one mole of
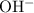`\rm OH^(-)` ions will be released.

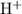`\rm H^(+)` ions and
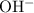`\rm OH^(-)` ions neutralize each other at a one-to-one ratio. Therefore, when one mole of the diprotic acid
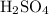`\rm H_2SO_4` dissolves in water completely, it will take two moles of
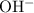`\rm OH^(-)` to neutralize that two moles of
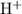`\rm H^(+)` produced. On the other hand, two moles formula units of the monoprotic base
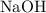`\rm NaOH` will be required to produce that two moles of
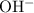`\rm OH^(-)`. Therefore,
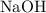`\rm NaOH` and
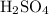`\rm H_2SO_4` formula units would neutralize each other at a two-to-one ratio.

`\rm H_2SO_4 + 2\; NaOH \to Na_2SO_4 + 2\; H_2O`.

`\displaystyle \frac{n(\mathrm{NaOH})}{n(\mathrm{H_2SO_4})} = (2)/(1) = 2`.

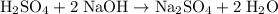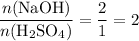Previous calculations show that
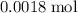`0.0018\; \rm mol` of
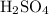`\rm H_2SO_4` was produced. Calculate the number of moles of
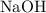`\rm NaOH` formula units required to neutralize that

`\begin{aligned}n(\mathrm{NaOH}) &= \frac{n(\mathrm{NaOH})}{n(\mathrm{H_2SO_4})}\cdot n(\mathrm{H_2SO_4}) \\&= 2 * 0.0018\; \rm mol = 0.0036\; \rm mol\end{aligned}`.

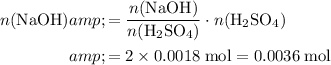Calculate the concentration of a
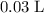`0.03\; \rm L` solution that contains exactly
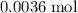`0.0036\; \rm mol` of
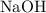`\rm NaOH` formula units:

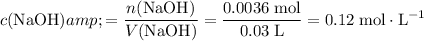`\begin{aligned}c(\mathrm{NaOH}) &= \frac{n(\mathrm{NaOH})}{V(\mathrm{NaOH})} = (0.0036\; \rm mol)/(0.03\; \rm L) = 0.12\; \rm mol \cdot L^(-1)\end{aligned}`.