Question

DF is the angle bisector of ADE. Determine the value of x. ANSWERS: A) – 8 B) 8 C) – 4 D) 4

Answer 1

`x = 4`

Answer D is correct.

Explanation:

( ADF angle = FDE angle)

[Because DF is the angle bisector]

`9x - 1 = 8x + 3`

`9x - 8x = 1 + 3 \\ x = 4`

hope this helps you.

Answer 2

D)
`x=4 \textdegree`

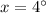
Explanation:

Before answering this question, we must first understand what an angle bisector is. An angle bisector is any ray, line, or line segment that splits an angle into two congruent, smaller angles.

That being said, since
`DF` bisects
`\angle ADE`, we can say that
`\angle ADF \cong \angle FDE`. If you'll remember, congruent angles have equal measures, so
`m\angle ADF = m\angle FDE`.

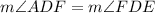Substituting the given values of the angle measures into the equation and solving, we get:

`9x-1=8x+3`

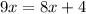`9x=8x+4` (Add 1 to both sides)

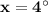`\bf x = 4 \textdegree` (Subtract 8x from both sides)

Hope this helps!