Question

(08.01) Two lines, A and B, are represented by the following equations: Line A: 3x + 3y = 12 Line B: x + y = 4 Which statement is true about the solution to the set of equations? It is (12, 4). There are infinitely many solutions. It is (4, 12). There is no solution.

Answer 1

Answer: There are infinitely many solutions.

Explanation:

Given, Two lines, A and B, are represented by the following equations:

Line A: 3x + 3y = 12

Line B: x + y = 4

By comparing to the equations
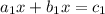`a_1x+b_1x=c_1` and
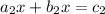`a_2x+b_2x=c_2` respectively , we have

`a_1=3,\ b_1=3\ \ \&\ c_1=12\\\\a_2=1,\ b_2=1\ \ \&\ c_2=4`

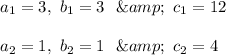
Now ,
`(a_1)/(a_2)=(3)/(1),\ (b_1)/(b_2)=(3)/(1),\ \&\ (c_1)/(c_2)=(12)/(4)=(3)/(1)`

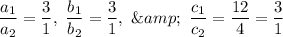
i.e.
`(a_1)/(a_2)=(b_1)/(b_2)=(c_1)/(c_2)`

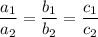
It implies the gives lines are co-incident (linearly dependent).

That means it has infinitely many solutions.

So, the correct answer is "There are infinitely many solutions.".