Question

An electron moves at a speed of 1.0 x 104 m/s in a circular path of radius 2 cm inside a solenoid. The magnetic field of the solenoid is perpendicular to the plane of the electron’s path. Calculate (a) the strength of the magnetic field inside the solenoid and (b) the current in the solenoid if it has 25 turns per centimeter.

Answer 1

(a) B = 2.85 ×
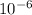`10^(-6)` Tesla

(b) I = I = 0.285 A

Step-by-step explanation:

a. The strength of magnetic field, B, in a solenoid is determined by;

r =
`(mv)/(qB)`

⇒ B =
`(mv)/(qr)`

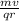
Where: r is the radius, m is the mass of the electron, v is its velocity, q is the charge on the electron and B is the magnetic field

B =
`\frac{9.11*10^{-31*1.0*10^(4) } }{1.6*10^(-19)*0.02 }`

=
`(9.11*10^(-27) )/(3.2*10^(-21) )`

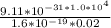
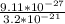
B = 2.85 ×
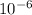`10^(-6)` Tesla

b. Given that; N/L = 25 turns per centimetre, then the current, I, can be determined by;

B = μ I N/L

⇒ I = B ÷ μN/L

where B is the magnetic field, μ is the permeability of free space = 4.0 ×
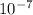`10^(-7)`Tm/A, N/L is the number of turns per length.

I = B ÷ μN/L

=
`(2.85*10^(-6) )/(4*10^(-7) *25)`

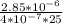
I = 0.285 A