Question

which of the following options represents the desired result when using synthetic division to find out the upper bound of the polynomials F(x)=x^3+4x^2+x-6 ?

Answer 1

Option (C)

Explanation:

Given function is F(x) = x³+ 4x² + x - 6

Possible rational zeros of this function =
`(\pm1,\pm2,\pm3,\pm6)/(\pm1)`

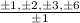
[Possible rational zeros of a function f(x) = ax³+ bx² + cx + d,

=
`\frac{\text{factors of d}}{\text{factors of a}}`]

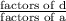Let the possible zero of this function is 2.

Now do the synthetic division,

2| 1 4 1 -6

↓ 2 12 26

1 6 13 20

Here all the numbers at the bottom are positive by dividing with a positive number 2, therefore, 2 is the upper bound.

There will be no rational zero (Positive) above 2.

Therefore, Option (C) will be the answer.