In ΔRST, the measure of ∠T=90°, ST = 44 feet, and TR = 84 feet. Find the measure of ∠R to the nearest tenth of a degree.

Question

asked Jul 13, 2021 216k views

2 Answers

Amit Amola · Answer 1 · 2021-07-19T06:38:20+0000

Answer:

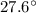
$27.6^\circ$

Explanation:

Given:

A
$\triangle RST$ with
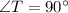
$\angle T =90 ^\circ$

ST = 44 feet

TR = 84 feet

To find:

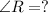
$\angle R = ?$

Solution:

Please have a look at the attached figure for clear view of the given dimensions of the right angled triangle.

Here, we can use trigonometric formula to find out the
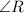$\angle R$ .

We know that formula for tangent of angle
$\theta$ is given as:

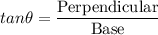
$tan \theta = \frac{\text{Perpendicular}}{\text{Base}}$

Here, Perpendicular for
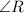$\angle R$ is side ST and

Base is side TR.

Putting the values in above tangent formula:

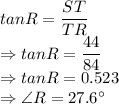
$tan R = (ST)/(TR)\\\Rightarrow tan R = (44)/(84)\\\Rightarrow tan R = 0.523\\\Rightarrow \angle R = 27.6^\circ$

Hence,
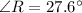$\angle R = 27.6^\circ$ is the answer.