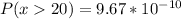Question

A multiple-choice standard test contains total of 25 questions, each with four answers. Assume that a student just guesses on each question and all questions are answered independently. (a) What is the probability that the student answers more than 20 questions correctly

Answer 1

`P(x>20)=9.67*10^(-10)`

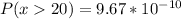
Explanation:

If we call x the number of correct answers, we can said that P(x) follows a Binomial distribution, because we have 25 questions that are identical and independent events with a probability of 1/4 to success and a probability of 3/4 to fail.

So, the probability can be calculated as:

`P(x)=nCx*p^(x)*q^(n-x)=25Cx*0.25^(x)*0.75^(25-x)`

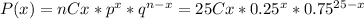
Where n is 25 questions, p is the probability to success or 0.25 and q is the probability to fail or 0.75.

Additionally,
`25Cx=(25!)/(x!(25-x)!)`

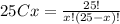
So, the probability that the student answers more than 20 questions correctly is equal to:

`P(x>20)=P(21)+P(22)+P(23)+P(24)+P(25)`

Where, for example, P(21) is equal to:

`P(21)=25C21*0.25^(21)*0.75^(25-21)=9.1*10^(-10)`

Finally, P(x>20) is equal to:

`P(x>20)=9.67*10^(-10)`