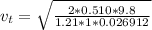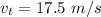Question

510 g squirrel with a surface area of 935 cm2 falls from a 4.8-m tree to the ground. Estimate its terminal velocity. (Use the drag coefficient for a horizontal skydiver. Assume that the squirrel can be approximated as a rectanglar prism with cross-sectional area of width 11.6 cm and length 23.2 cm. Note, the squirrel may not reach terminal velocity by the time it hits the gr

Answer 1

The terminal velocity is
`v_t =17.5 \ m/s`

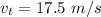
Step-by-step explanation:

From the question we are told that

The mass of the squirrel is
`m_s = 50\ g = (50)/(1000) = 0.05 \ kg`

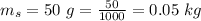
The surface area is
`A_s = 935 cm^2 = (935)/(10000) = 0.0935 \ m^2`

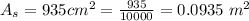
The height of fall is h =4.8 m

The length of the prism is
`l = 23.2 = 0.232 \ m`

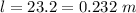
The width of the prism is
`w = 11.6 = 0.116 \ m`

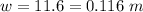
The terminal velocity is mathematically represented as

`v_t = \sqrt{(2 * m_s * g )/(\dho_s * C * A ) }`

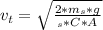
Where
`\rho` is the density of a rectangular prism with a constant values of
`\rho = 1.21 \ kg/m^3`

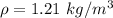
`C` is the drag coefficient for a horizontal skydiver with a value = 1

A is the area of the prism the squirrel is assumed to be which is mathematically represented as

`A = 0.116 * 0.232`

`A = 0.026912 \ m^2`

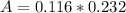
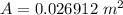
substituting values

`v_t = \sqrt{(2 * 0.510 * 9.8 )/(1.21 * 1 * 0.026912 ) }`

`v_t =17.5 \ m/s`