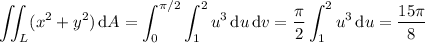Question

Find the mass of lamina bounded by circles x2 + y2 = 1 and x2 + y2 = 4in the first quadrant if the density is (x2 + y2). Could please anyone solve this...

Answer 1

Since density is equal to mass per unit volume, mass is equal to density times volume. So we split up the lamina into tiny regions with "volume" (area) equal to dA, multiplied by the density, and integrated over the entirety of the lamina.

This is best done in polar coordinates:

`\begin{cases}x=u\cos v\\y=u\sin v\end{cases}\implies\mathrm dA=\mathrm dx\,\mathrm dy=u\,\mathrm du\,\mathrm dv`

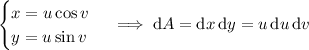
so that
`x^2+y^2=u^2\cos^2v+u^2\sin^2v=u^2`.

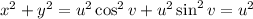The lamina is then the set of points

`L=\left\{(u,v)\mid1\le u\le2\land0\le v\le\frac\pi2\right\}`

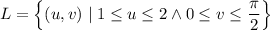
Now compute the integral: the mass of the lamina is

`\displaystyle\iint_L(x^2+y^2)\,\mathrm dA=\int_0^(\pi/2)\int_1^2u^3\,\mathrm du\,\mathrm dv=\frac\pi2\int_1^2u^3\,\mathrm du=\frac{15\pi}8`