Question

A company has a policy of retiring company cars; this policy looks at number of miles driven, purpose of trips, style of car and other features. The distribution of the number of months in service for the fleet of cars is bell-shaped and has a mean of 51 months and a standard deviation of 11 months. Using the Empirical Rule rule, what is the approximate percentage of cars that remain in service between 73 and 84 months

Answer 1

The approximate percentage of cars that remain in service between 73 and 84 months

P( 73 < x < 84 ) = 0.02145 = 2.1 %

Step-by-step explanation:

Step-by-step explanation:-

Given mean of the Population 'μ ' = 51 months

Standard deviation of the Population 'σ' = 11 months

Let 'X' be the random variable of Normal distribution

Let 'X' = 73

`Z = (x-mean)/(S.D) = (73-51)/(11) = 2`

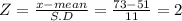
Let 'X' = 84

`Z = (84-51)/(11) = 3`

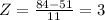
The approximate percentage of cars that remain in service between 73 and 84 months

P( 73 < x < 84 ) = P( 2 < Z < 3)

= P( Z<3) - P( Z <2)

= 0.5 + A(3) - ( 0.5 + A(2))

= A(3) - A( 2)

= 0.49865 - 0.4772 ( From Normal table)

= 0.02145

P( 73 < x < 84 ) = 0.02145

The approximate percentage of cars that remain in service between 73 and 84 months

P( 73 < x < 84 ) = 0.02145 = 2.1 %