Question

Find the measurements (the length L and the width W) of an inscribed rectangle under the line with the 1st quadrant of the x & y coordinate system such that the area is maximum. Also, find that maximum area. To get full credit, you must draw the picture of the problem and label the length and the width in terms of x and y.

Answer 1

The question is incomplete. Here is the complete question.

Find the measurements (the lenght L and the width W) of an inscribed rectangle under the line y = -
`(3)/(4)`x + 3 with the 1st quadrant of the x & y coordinate system such that the area is maximum. Also, find that maximum area. To get full credit, you must draw the picture of the problem and label the length and the width in terms of x and y.

Answer: L = 1; W = 9/4; A = 2.25;

Explanation: The rectangle is under a straight line. Area of a rectangle is given by A = L*W. To determine the maximum area:

A = x.y

A = x(-
`(3)/(4).x + 3`)

A = -
`(3)/(4).x^(2) + 3x`

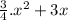
To maximize, we have to differentiate the equation:

`(dA)/(dx)` =
`(d)/(dx)`(-
`(3)/(4).x^(2) + 3x`)

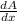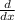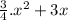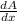`(dA)/(dx)` = -3x + 3

The critical point is:

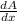`(dA)/(dx)` = 0

-3x + 3 = 0

x = 1

Substituing:

y = -
`(3)/(4)`x + 3

y = -
`(3)/(4)`.1 + 3

y = 9/4

So, the measurements are x = L = 1 and y = W = 9/4

The maximum area is:

A = 1 . 9/4

A = 9/4

A = 2.25