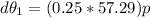Question

You stand a known distance from the base of the tree, measure the angle of elevation the top of the tree to be 15◦ , and then compute the height of the tree above eye level. Use the appropriate linear approximation to estimate the maximum possible error in your measurement of the angle (measuered in degrees) to be sure that your computation of the height has a relative error of at most ±p%. Give an exact answer, simplified as much as possible. Do not use a calculator. Assume p ∼ 0.

Answer 1

The maximum possible error of in measurement of the angle is
`d\theta_1 =(14.36p)^o`

Explanation:

From the question we are told that

The angle of elevation is
`\theta_1 = 15 ^o = (\pi)/(12)`

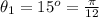
The height of the tree is h

The distance from the base is D

h is mathematically represented as

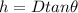`h = D tan \theta` Note : this evaluated using SOHCAHTOA i,e

`tan\theta = (h)/(D)`

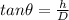
Generally for small angles the series approximation of
`tan \theta \ is`

`tan \theta = \theta + (\theta ^3 )/(3)`

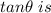
So given that
`\theta = 15 \ which \ is \ small`

`h = D (\theta + (\theta^3)/(3) )`

`dh = D (1 + \theta^2) d\theta`

=>
`(dh)/(h) = (1 + \theta ^2)/(\theta + (\theta^3)/(3) ) d \theta`

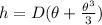
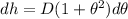
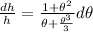
Now from the question the relative error of height should be at most

`\pm p`%

=>
`(dh)/(h) = \pm p`

=>
`(1 + \theta ^2)/(\theta + (\theta^3)/(3) ) d \theta = \pm p`

=>
`d\theta = \pm (\theta + (\theta^3)/(3) )/(1+ \theta ^2) * \ p`

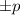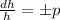
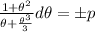
So for
`\theta_1`

`d\theta_1 = \pm (\theta_1 + (\theta^3_1 )/(3) )/(1+ \theta_1 ^2) * \ p`

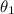
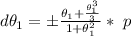
substituting values

`d [(\pi)/(12) ] = \pm ([(\pi)/(12) ] + ([(\pi)/(12) ]^3 )/(3) )/(1+ [(\pi)/(12) ] ^2) * \ p`

=>
`d\theta_1 = 0.25 p`

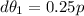
Converting to degree

`d\theta_1 = (0.25* 57.29) p`

`d\theta_1 =(14.36p)^o`