Question

?ABC is an isosceles triangle with legs AB and AC. ?AYX is also an isosceles triangle with legs AY and AX. The proof that ?ABC ~ ?AYX is shown. Statements Reasons 1. ?ABC is isosceles with legs AB and AC; ?AYX is also isosceles with legs AY and AX. 1. Given 2. AB ? AC and AY ? AX 2. Definition of isosceles triangle 3. AB = AC and AY = AX 3. Definition of congruency 4. AY • AC = AX • AC 4. Multiplication property of equality 5. AY • AC = AX • AB 5. Substitution property of equality 6. 6. Division property of equality 7. 7. Division property of equality 8. ? 8. ? 9. ?ABC ~ ?AYX 9. SAS similarity theorem Which statement and reason are missing in the proof? ?A ? ?A; reflexive property ?X ? ?X; reflexive property ?ABC ? ?AYX; corresponding angles of similar triangles ?ABC ? ?AXY; corresponding angles of similar triangles

Answer 1

∠A ≅ ∠A; reflexive property

Explanation:

i got it right on the unit test..

Answer 2

The correct option is;

∠A ≅ ∠A ; reflective property

Explanation:

1. ΔABC is isosceles with legs AB and AC

ΔAYX is also isosceles with legs AY and AX

2. AB ≅ AC and AY ≅ AX (Definition of isosceles triangle)

3. AB = AC and AY = AX (Definition of congruency)

4. AY · AC = AX · AC (Multiplication property of equality)

5. AY · AC = AX · AB (Substitution property of equality)

6.
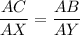`(AC)/(AX) = (AB)/(AY)` (Division property of equality)

7.
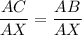`(AC)/(AX) = (AB)/(AX)` (Division property of equality)

8. ∠A ≅ ∠A ; reflective property

9. ΔABC ~ ΔAXY SAS similarity theorem (The two triangles have the same vertex angle A hence they are similar based on the Side Angle Side theorem for uniqueness of triangles.