Answer:
The measure of angle BCD is
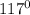 .
.
Explanation:
A parallelogram is a four sided shape with equal and parallel sides.
From the given dimension, we have two triangles ABC and ADC.
From ΔABC, applying the cosine rule;
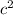 =
=
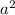 +
+
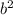 - 2ab Cos C
- 2ab Cos C
Let a = 28, b = 26 and c = 20. So that;
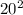 =
=
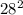 +
+
 - 2 × 28 × 26 Cos C
- 2 × 28 × 26 Cos C
400 = 784 + 676 - 1450 Cos C
400 = 1460 - 1450 Cos C
1450 Cos C = 1460 - 400
1450 Cos C = 1060
Cos C = 0.7310
C =

⇒ <ACB =

Also from ΔADC, applying the Cosine rule;
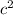 =
=
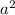 +
+
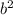 - 2ab Cos C
- 2ab Cos C
Let a = 20, b = 26 and c = 28
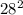 =
=
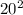 +
+
 - 2 × 20 × 26 Cos C
- 2 × 20 × 26 Cos C
784 = 400 + 676 - 1040 Cos C
784 = 1076 - 1040 Cos C
1040 Cos C = 1076 - 784
1040 Cos C = 292
Cos C = 0.2808
C =
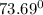
⇒ <ACD =
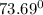
<BCD = <ACB + <ACD
=
 +
+
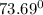
=
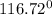
The measure of angle BCD is
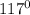 .
.