According to the Rational Root Theorem, which number is a potential root of f(x) = 9x8 + 9x6 – 12x + 7?

Question

asked Dec 11, 2021 29.4k views

2 Answers

Paul Dragoonis · Answer 1 · 2021-12-15T16:40:54+0000

Answer:

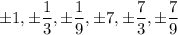$\pm 1, \pm(1)/(3),\pm(1)/(9),\pm 7, \pm(7)/(3),\pm(7)/(9)$ .

Explanation:

According to the Rational Root Theorem, the potential roots of a polynomial are

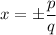
$x=\pm(p)/(q)$

where, p is a factor of constant and q is a factor of leading term.

The given polynomial is

f(x)=9x^8+9x^6-12x+7

Here, 9 is the leading term and 7 is constant.

Factors of 9 are ±1, ±3, ±9.

Factors of 7 are ±1, ±7.

Using rational root theorem, the rational or potential roots are

$x=\pm 1, \pm(1)/(3),\pm(1)/(9),\pm 7, \pm(7)/(3),\pm(7)/(9)$

Therefore, the potential root of f(x) are
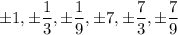$\pm 1, \pm(1)/(3),\pm(1)/(9),\pm 7, \pm(7)/(3),\pm(7)/(9)$ .