Question

A classic counting problem is to determine the number of different ways that the letters of "misspell" can be arranged. Find that number.

Answer 1

10,080 different ways that the letters of "misspell" can be arranged.

Explanation:

Number of arrangents of the letters of a word:

A word has n letters.

The are m repeating letters, each of them repeating
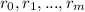`r_(0), r_(1), ..., r_(m)` times

So the number of distincts ways the letters can be arranged is:

`N_(A) = (n!)/(r_(1)! * r_(2)! * ... * r_(m))`

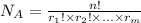
In this question:

Misspell has 8 letters, with s and l repeating twice.

So

`N_(A) = (8!)/(2!2!) = 10080`

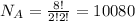
10,080 different ways that the letters of "misspell" can be arranged.