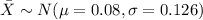Question

In a manufacturing process, a machine produces bolts that have an average length of 5 inches with a variance of .08. If we randomly select five bolts from this process, what is the standard deviation of the sampling distribution of the sample mean

Answer 1

`\bar X \sim N(\mu , (\sigma)/(√(n)))`

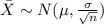
And replacing:

`\mu_(\bar X)= 5`

And the deviation:

`\sigma_(\bar X)= (0.283)/(√(5))= 0.126`

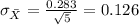
And the distribution is given:

`\bar X \sim N(\mu= 0.08, \sigma= 0.126)`

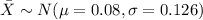
Explanation:

For this case we have the following info given :

`\mu= 5. \sigma^2 =0.08`

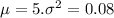
And the deviation would be
`\sigma = √(0.08)= 0.283`

For this case we select a sample size of n = 5 and the distirbution for the sample mean would be:

`\bar X \sim N(\mu , (\sigma)/(√(n)))`

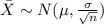
And replacing:

`\mu_(\bar X)= 5`

And the deviation:

`\sigma_(\bar X)= (0.283)/(√(5))= 0.126`

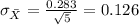
And the distribution is given:

`\bar X \sim N(\mu= 0.08, \sigma= 0.126)`