Answer:
a). r =

b). At least 5 terms should be added.
Explanation:
Formula representing sum of infinite geometric sequence is,

Where a = first term of the sequence
r = common ratio
a). If the sum is seven times the value of its first term.
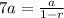
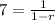
7(1 - r) = 1
7 - 7r = 1
7r = 7 - 1
7r = 6
r =

b). Since sum of n terms of the geometric sequence is given by,

If the sum of n terms of this sequence is more than half the value of the infinite sum.
![(a[1-((6)/(7))^(n)])/(1-(6)/(7))](https://img.qammunity.org/2021/formulas/mathematics/college/m4chbfenchquusxerkffrpmu7a5nx38ksi.png) >
>
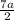
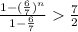
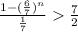
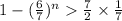
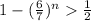

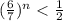
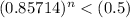
n[log(0.85714)] < log(0.5)
-n(0.06695) < -0.30102
n >
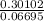
n > 4.496
n > 4.5
Therefore, at least 5 terms of the sequence should be added.