Question

Quick Start Company makes a 12-volt car batteries. After many years of product testing, the company knows the average life of a Quick Start battery is normally distributed, with mean=45 months and a std. deviation = 8 months.

If Quick start guarantees a full refund on any battery that fails within the 36 month period after purchase, what percentage of its batteries will the company expect to replace?

If quick Start does not want to make refunds for more than 10% ofits batteries under the full refund guarantee policy, for how longshould the company guarantee the batteries (to the nearest month)

Answer 1

The company will expect to replace 13.03% of batteries.

The company should guarantee the batteries for 35 months.

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this question, we have that:

`\mu = 45, \sigma = 8`

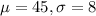
If Quick start guarantees a full refund on any battery that fails within the 36 month period after purchase, what percentage of its batteries will the company expect to replace?

This is the pvalue of Z when X = 36. So

`Z = (X - \mu)/(\sigma)`

`Z = (36 - 45)/(8)`

`Z = -1.125`

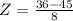
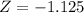
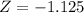`Z = -1.125` has a pvalue of 0.1303.

The company will expect to replace 13.03% of batteries.

If quick Start does not want to make refunds for more than 10% ofits batteries under the full refund guarantee policy, for how longshould the company guarantee the batteries

They should guarantee to the 10th percentile, which is X when Z has a pvalue of 0.1. So it is X when Z = -1.28.

`Z = (X - \mu)/(\sigma)`

`-1.28 = (X - 45)/(8)`

`X - 45 = -1.28*8`

`X = 34.76`

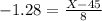
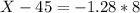
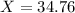
Rounding to the nearest month

The company should guarantee the batteries for 35 months.