Question

According to data from a medical​ association, the rate of change in the number of hospital outpatient​ visits, in​ millions, in a certain country each year from 1980 to the present can be approximated by f’(t) = 0.001155t(t-1980)^0.50, where t is the year.

a. Using the fact that in 1980 there were 264,034,000 outpatient​ visits, find a formula giving the approximate number of outpatient visits as a function of time.
b. Use the answer to part a to forecast the number of outpatient visits in the year 2015.

Answer 1

a)
`f(t)=0.001155[(2)/(3)t(t-1980)^(3/2)-(4)/(15)(t-1980)^(5/2)]+264,034,000`

b) f(t=2015) = 264,034,317.7

Explanation:

The rate of change in the number of hospital outpatient​ visits, in​ millions, is given by:

`f'(t)=0.001155t(t-1980)^(0.5)`

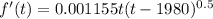
a) To find the function f(t) you integrate f(t):

`\int (df(t))/(dt)dt=f(t)=\int [0.001155t(t-1980)^(0.5)]dt`

To solve the integral you use:

`\int udv=uv-\int vdu\\\\u=t\\\\du=dt\\\\dv=(t-1980)^(1/2)dt\\\\v=(2)/(3)(t-1980)^(3/2)`

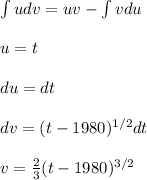
Next, you replace in the integral:

`\int t(t-1980)^(1/2)=t((2)/(3)(t-1980)^(3/2))- (2)/(3)\int(t-1980)^(3/2)dt\\\\= (2)/(3)t(t-1980)^(3/2)-(4)/(15)(t-1980)^(5/2)+C`

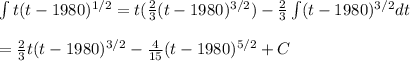
Then, the function f(t) is:

`f(t)=0.001155[(2)/(3)t(t-1980)^(3/2)-(4)/(15)(t-1980)^(5/2)]+C'`

The value of C' is deduced by the information of the exercise. For t=0 there were 264,034,000 outpatient​ visits.

Hence C' = 264,034,000

The function is:

`f(t)=0.001155[(2)/(3)t(t-1980)^(3/2)-(4)/(15)(t-1980)^(5/2)]+264,034,000`

b) For t = 2015 you have:

`f(t=2015)=0.001155[(2)/(3)(2015)(2015-1980)^(1/2)-(4)/(15)(2015-1980)^(5/2)]+264,034,000\\\\f(t=2015)=264,034,317.7`