Question

F(x) = x^2-3x+18f(x)=x 2 −3x+18f, left parenthesis, x, right parenthesis, equals, x, squared, minus, 3, x, plus, 18 What is the value of the discriminant of fff? How many distinct real number zeros does fff have?

Answer 1

The discriminant value of F is -63

F has 0 distinct real number zeros

Explanation:

Answer 2

No real roots or no real zeros.

Explanation:

The given function is

`f(x)=x^2-3x+18`

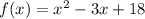
We need to find the number of real zeroes.

The given function is a quadratic function.

Let a quadratic function is
`f(x)=ax^2+bx+c`.

If
`b^2-4ac<0`, then the function has no real root.

If
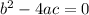`b^2-4ac=0`, then the function has one real root with multiplicity 2.

If
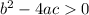`b^2-4ac>0`, then the function has two real roots.

In the given function,

`a=1,b=-3,c=18`

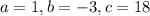
So,

`b^2-4ac=(-3)^2-4(1)(18)=9-72=-63<0`

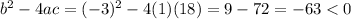
The value of discriminant is -63.

Therefore, the given function has no real root or no real zeros.