Question

HELP!

Consider the below equation:

0.5x-7= sqrt(-5x+29)


Give 2 different ways to show that the equation does not have any solutions. One way must be solving algebraically, and the other way must be by graphing.

Answer 1

The answer to this question can be described as follows:

Explanation:

Given equation:

`\bold{0.5x-7= √((-5x+29))}`

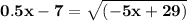
As in the given question the two ways to solve the equation can be defined as follows:

First way:

Let square the above-given equation then we will get:

`\to (0.5x-7)^2= (√((-5x+29)))^2\\\\\to (0.5x)^2 +7^2-2* 0.5x* 7= -5x+29\\\\\to 0.25x^2 +49- 7x= -5x+29\\\\\to 0.25x^2 - 7x+5x +49-29=0\\\\\to 0.25x^2 - 2x+20=0\\\\`

The calculated equation doesn't have any like term that's why it can't be factorised.

Second way:

after calculating the equation that is
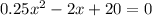`0.25x^2-2x+20=0`, it graph is given in attachment please find.