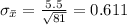Question

A population has a standard deviation of 5.5. What is the standard error of the sampling distribution if the sample size is 81?

Answer 1

`\sigma = 5.5`

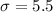
And we have a sample size of n =81. We want to estimate the standard error of the sampling distribution
`\bar X` and for this case we know that the distribution is given by:

`\bar X \sim N(\mu ,(\sigma)/(√(n)))`

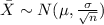
And the standard error would be:

`\sigma_(\bar x)= (\sigma)/(√(n))`

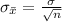
And replacing we got:

`\sigma_(\bar x)=(5.5)/(√(81))= 0.611`

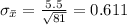
Explanation:

For this case we know the population deviation given by:

`\sigma = 5.5`

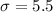
And we have a sample size of n =81. We want to estimate the standard error of the sampling distribution
`\bar X` and for this case we know that the distribution is given by:

`\bar X \sim N(\mu ,(\sigma)/(√(n)))`

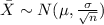
And the standard error would be:

`\sigma_(\bar x)= (\sigma)/(√(n))`

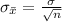
And replacing we got:

`\sigma_(\bar x)=(5.5)/(√(81))= 0.611`