Question

The driver of a car traveling along a straight, flat road applies the brakes, which produce a constant acceleration ofspace a (t )thin space equals space minus 20 space f t divided by s e c squared. If the car is traveling at 80 feet per second when the driver applies the brakes, how far does the car travel between the time the brakes are applied and the time the car comes to a stop

Answer 1

x = 160 ft

Explanation:

The distance traveled by the car between the time the brakes are applied and the time the car comes to a stop is given by:

`v_(f)^(2) = v_(0)^(2) + 2ax`

Where:

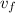`v_(f)`: is the final speed of the car = 0 (since it stops)

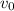`v_(0)`: is the initial speed of the car = 80 ft/s

a: is the acceleration of the car = -20 ft/s²

x: is the distance recorred by the car

The distance traveled by the car between the time the brakes are applied and the time the car comes to a stop is:

`x = (v_(f)^(2) - v_(0)^(2))/(2a) = (0 - (80 ft/s)^(2))/(2*(-20 ft/s^(2))) = 160 ft`

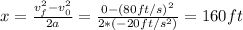
Therefore, the car travels 160 ft between the time the brakes are applied and the time the car comes to a stop.

I hope it helps you!