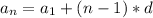Question

Indicate the general rule for this sequence. Find a1 and the common difference. a4 = 18 a7 = 9

Answer 1

`a_(n) = 27 - 3(n-1)`

Explanation:

Arithmetic sequences concepts:

The general rule of an arithmetic sequence is the following:
`a_(n+1) = a_(n) + d`

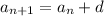
In which d is the common diference between each term.

We can expand the general equation to find the nth term from the first, by the following equation:

`a_(n) = a_(1) + (n-1)*d`

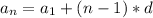
And also:

`a_(n) = a_(m) + (n-m)*d`

In this question:

`a_(4) = 18, a_(7) = 9`

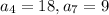
Finding the common ratio:

`a_(n) = a_(m) + (n-m)*d`

`a_(7) = a_(4) + (7-4)*d`

`9 = 18 + 3d`

`3d = -9`

`d = (-9)/(3)`

`d = -3`

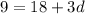
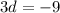
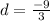
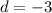
Finding the first term:

`a_(4) = a_(1) + (4-1)*d`

`18 = a_(1) + 3*(-3)`

`a_(1) = 27`

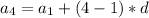
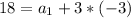
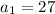
General rule:

`a_(n) = a_(1) + (n-1)*d`

`a_(n) = 27 - 3(n-1)`