Question

Which is not a root of z3 + 8 = 0?

a. 2
b. -2
c. 1+1
d. 1-1-13
Please select the best answer from the choices provided
A
B
C
D

Answer 1

Answer: A. 2

=================================================

Short explanation:

Plug z = 2 into the equation and you'll find that

z^3 + 8 = 2^3 + 8 = 8+8 = 16

but the result should be 0 since the original equation has 0 on the right side. Therefore, z = 2 is not a solution.

------------------------------------

Longer explanation:

Solve the equation for z to find the three roots.

z^3 + 8 = 0

(z+2)(z^2 - 2z + 4) = 0 ... sum of cubes factoring rule

z+2 = 0 or z^2 - 2z + 4 = 0

z = -2 or z^2 - 2z + 4 = 0

We see that z = -2 is one root. To find the other two roots, use the quadratic formula to solve z^2 - 2z + 4 = 0 for z

`z = (-b\pm√(b^2-4ac))/(2a)\\\\z = (-(-2)\pm√((-2)^2-4(1)(4)))/(2(1))\\\\z = (2\pm√(-12))/(2)\\\\z = (2\pm√(-1*4*3))/(2)\\\\z = (2\pm√(-1)*√(4)*√(3))/(2)\\\\z = (2\pm i*2*√(3))/(2)\\\\z = (2\pm 2i*√(3))/(2)\\\\z = (2(1\pm i*√(3)))/(2)\\\\z = 1\pm i√(3)\\\\z = 1+ i√(3) \ \text{ or } \ z = 1- i√(3)\\\\`

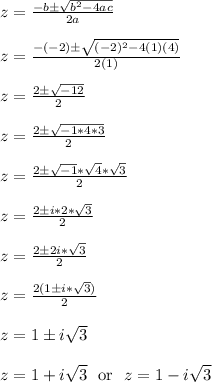
Therefore, the three roots of z^3+8=0 are
`z = -2, \ z = 1+i√(3), \ z=1-i√(3)`

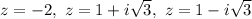
The value z = 2 is not part of the list of solutions.

We can verify each solution by plugging it back into the original equation. For instance, with z = -2, we get

z^3 + 8 = 0

(-2)^3+8 = 0

-8+8 = 0

0 = 0 ... solution is confirmed.

I'll let you check the other solutions.