Question

The restrooms for the former Estabrook Hall were known to each be 117 cubic feet in volume. We are tasked with creating a 1:4 scale model of one of the rooms. For the purposes of this analysis, we'll treat the facilities like simple rectangular boxes. What is the volume of the model in cubic inches? If the model has a floor area of 117 sq. Inches, what is the height of the real facility? (include units with answer)

Answer 1

1) The volume of the model is 3159 in.³

2) The height of the real facility is 61.94 ft

Explanation:

1) The parameters given are;

Volume of the Estabrook hall = 117 ft³

Scale of model = 1:4

For the scale factor of a volume, we have;

`Volume \, scale \, factor =\left ((a)/(b) \right )^3 = \left ((1)/(4) \right )^3 = (1)/(64)`

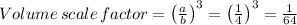
That is the volume of the model is 1/64 times the volume of the actual Estabrook hall restrooms or

`(1)/(64) * 117 \, ft^3= 1\tfrac{53}{64} \, ft^3`

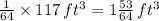
∴ The volume of the model = 1.83 ft.³

1 ft.³ = 1728 in.³

∴ 1.83 ft.³ = 1.83 ft.³ × 1728 in.³/ft.³ = 3159 in.³

2) Where the model of the floor has an area of 117 in.²

Therefore, since the volume of a rectangular prism shape = Floor area × Height, we have

The height, h = Volume/(floor area) = 3159/117 = 185.8 in.

From a scale of 1:4, we have that the height of the real facility = 4 × 185.8 in.

Hence, the height of the real facility = 743.3 in = 61.94 ft.