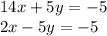Question

The equations 2 x minus 5 y = negative 5, 11 x minus 5 y = 15, 9 x + 5 y = 5, and 14 x + 5 y = negative 5 are shown on the graph below.

On a coordinate plane, there are 4 lines. Green line goes through (2, 1.5) and (0.5, negative 2). Blue line goes through (0, 1) and (0.5, 0). Pink line goes through (negative 1, 2), and (0, negative 1). Orange line goes through (0, 1) and (2, 1.75).

Which system of equations has a solution of approximately (–0.6, 0.8)?

Answer 1

B

Explanation:

Answer 2

`14x+5y=-5\\2x-5y=-5`

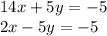
Explanation:

The given equations are

`2x-5y=-5\\11x-5y=15\\9x+5y=5\\14x+5y=-5`

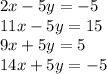
Let's demontrate that the system

`14x+5y=-5\\2x-5y=-5`

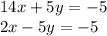
Has (-0.6, 0.8) as solution, approximately.

If we sum those equations, we have

`16x=-10\\x=(-10)/(16) \approx -0.625`

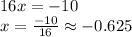
Then, we use this value to find the other one

`2x-5y=-5\\2(-0.625)-5y=-5\\-5y=-5+1.25\\y=(-3.75)/(-5) \approx 0.75`

As you can see, the answers aproximates to (-0.6, 0.8).

Therefore, the right system is

`14x+5y=-5\\2x-5y=-5`