Question

A closed container with volume of 7.20 L holds 10.9 g of liquid helium at 3.00 K and enough air to fill the rest of its volume at a pressure of 1.00 atm. The helium then evaporates and the container warms to room temperature (293 K). What is the final pressure inside the container?

Answer 1

The final pressure inside the container is 107.7 atm

Step-by-step explanation:

Given;

volume of the closed container = 7.20 L

mass of liquid helium in the container = 10.9 g

initial temperature of the container = 3.00 K

initial pressure of the container = 1.00 atm.

final temperature of the container = 293 K

Number of moles of He in the container = 10.9 / 4 = 2.725 moles

At 273˚K and 1 atm pressure (STP), the volume of 1 mole of a gas = 22.4 L

Volume of 2.725 moles of He at STP = 2.725 x 22.4 = 61.04 L

Volume of 2.725 moles of He at 3 K and 1 atm = (3/273) x 61.04 = 0.671 L

Thus, volume of He = 0.671 L

Volume of air in the container = 7.2 L – 0.671 L = 6.529 L

Since, the liquid helium evaporated, we only have air left in the container,

thus, final volume of the container, V₂ = 6.529 L

Initial volume of the container, V₁ = 7.20 L

Initial pressure of the in the container, P₁ = 1 atm

initial temperature of the container, T₁ = 3 K

Final temperature of the container, T₂ = 293 K

Final pressure of the container, P₂ = ?

Apply general gas law, in order to estimate P₂

`(P_1V_1)/(T_1) = (P_2V_2)/(T_2) \\\\P_2 = (P_1V_1T_2)/(T_1V_2) \\\\P_2 = (1*7.2*293)/(3* 6.529)\\\\P_2 = 107.7 \ atm`

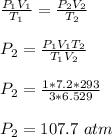
Therefore, the final pressure inside the container is 107.7 atm