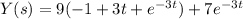Question

(10 points) Consider the initial value problem y′+3y=9t,y(0)=7. Take the Laplace transform of both sides of the given differential equation to create the corresponding algebraic equation. Denote the Laplace transform of y(t) by Y(s). Do not move any terms from one side of the equation to the other (until you get to part (b) below). = help (formulas) Solve your equation for Y(s). Y(s)=L{y(t)}=

Answer 1

The solution

`Y (s) = 9( -1 +3 t + e^(-3 t) ) + 7 e ^(-3 t)`

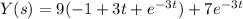
Explanation:

Explanation:-

Consider the initial value problem y′+3 y=9 t,y(0)=7

Step(i):-

Given differential problem

y′+3 y=9 t

Take the Laplace transform of both sides of the differential equation

L( y′+3 y) = L(9 t)

Using Formula Transform of derivatives

L(y¹(t)) = s y⁻(s)-y(0)

By using Laplace transform formula

`L(t) = (1)/(S^(2) )`

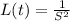
Step(ii):-

Given

L( y′(t)) + 3 L (y(t)) = 9 L( t)

`s y^(-) (s) - y(0) + 3y^(-)(s) = (9)/(s^(2) )`

`s y^(-) (s) - 7 + 3y^(-)(s) = (9)/(s^(2) )`

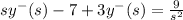
Taking common y⁻(s) and simplification, we get

`( s + 3)y^(-)(s) = (9)/(s^(2) )+7`

`y^(-)(s) = (9)/(s^(2) (s+3)+(7)/(s+3)`

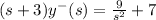
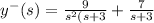
Step(iii):-

By using partial fractions , we get

`(9)/(s^(2) (s+3) = (A)/(s) + (B)/(s^(2) ) + (C)/(s+3)`

`(9)/(s^(2) (s+3) = (As(s+3)+B(s+3)+Cs^(2) )/(s^(2) (s+3))`

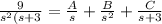
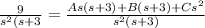
On simplification we get

9 = A s(s+3) +B(s+3) +C(s²) ...(i)

Put s =0 in equation(i)

9 = B(0+3)

B = 9/3 = 3

Put s = -3 in equation(i)

9 = C(-3)²

C = 1

Given Equation 9 = A s(s+3) +B(s+3) +C(s²) ...(i)

Comparing 'S²' coefficient on both sides, we get

9 = A s²+3 A s +B(s)+3 B +C(s²)

0 = A + C

put C=1 , becomes A = -1

`(9)/(s^(2) (s+3) = (-1)/(s) + (3)/(s^(2) ) + (1)/(s+3)`

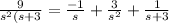
Step(iv):-

`y^(-)(s) = (9)/(s^(2) (s+3)+(7)/(s+3)`

`y^(-)(s) =9( (-1)/(s) + (3)/(s^(2) ) + (1)/(s+3)) + (7)/(s+3)`

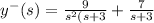
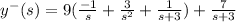
Applying inverse Laplace transform on both sides

`L^(-1) (y^(-)(s) ) =L^(-1) (9( (-1)/(s)) + L^(-1) ((3)/(s^(2) )) + L^(-1) ((1)/(s+3)) )+ L^(-1) ((7)/(s+3))`

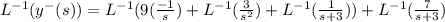
By using inverse Laplace transform

`L^(-1) ((1)/(s) ) =1`

`L^(-1) ((1)/(s^(2) ) ) = (t)/(1!)`

`L^(-1) ((1)/(s+a) ) =e^(-at)`

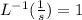
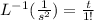
Final answer:-

Now the solution , we get

`Y (s) = 9( -1 +3 t + e^(-3 t) ) + 7 e ^(-3t)`