Question

What are the solutions of the equation sec(x)cot(x)= -2 on the interval [0,2pi]? Choose all correct answers.

Answer 1

The solutions are 7π/6 and 11π/6

Explanation:

Given the equation sec(x)cot(x)= -2 on the interval [0,2π]. In order to get the value of x, the following steps must be followed.

sec(x)cot(x)= -2

From trigonometry identity, sec(x)= 1/cos(x) and cot(x)= 1/tan(x) = cos(x)/sin(x)

subsituting this expressions in the given equation we have;

1/cos(x)*cos(x)/sin(x) = -2

1/sin(x) = -2

sin(x) = -1/2

`x = sin^(-1)-1/2\\ x = -30^(0)`

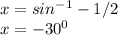
Since sin is negative in the 3rd and 4th quadrant,

In the 3rd quadrant, x = 180+30 = 210°

In the 4th quadrant, x = 360-30 = 330°

Converting the values to radian;

since 180° = πrad

210° = 210π/180 rad

210° = 7π/6 rad

Similarly, 330° = 330π/180 rad

330° = 11π/6 rad

The solutions are 7π/6 and 11π/6