Question

Jason and Melinda are both driving from Fort Worth, Texas, to Van Horn, Texas. Jason leaves at 8:30 and averages 60 mph (miles per hour) on the way. Melinda leaves at 9:00 and averages 70 mph on the way. The situation is modeled by this system, where x is the number of hours after melinda leaves and y is the distance each will travel : y=60 x+30 y=70 How long after Melinda leaves will she pass Jason, and how far will they each have traveled?

Answer 1

Melinda will pass Jackson 3 hours after she leaves.

They will have traveled 210 miles.

Explanation:

Answer 2

Melinda will pass Jackson 3 hours after she leaves.

They will have traveled 210 miles.

Explanation:

We need to build linear functions for their positions starting at 9 am.

We choose 9 am because it is the time of the last person leaving.

Melinda:

Leaves at 9 (from position 0).

Averages 70 mph.

So

`y_(M)(t) = 70t`

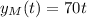
Jason:

Leaves at 8:30, 60 mph.

At 9, when Melinda leaves, 30 minutes(half an hour will have passed). He will be at the position 0.5*60 = 30. So

`y_(J)(t) = 30 + 60t`

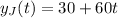
How long after Melinda leaves will she pass Jason

This is t for which:

`y_(M)(t) = y_(J)(t)`

`70t = 30 + 60t`

`10t = 30`

`t = (30)/(10)`

`t = 3`

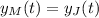
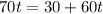
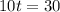
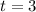
Melinda will pass Jackson 3 hours after she leaves.

How far will they each have traveled?

Either
`y_(M)(3)` or
`y_(J)(3)`. They are the same value.

`y_(M)(3) = 70*3 = 210`

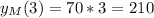
They will have traveled 210 miles.