Answer:
(a)96.77%
(b)3.23%
Explanation:
Starting with the Michaelis-Menten equation which is used to model biochemical reactions:
Dividing both sides by
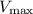
![(v)/(V_(max))=([S])/(K_M + [S])](https://img.qammunity.org/2021/formulas/mathematics/middle-school/y8ysjynzf56csbhd02k734bt1v0pexxzm1.png)
Where:
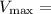 maximum rate achieved by the system
maximum rate achieved by the system
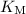 =The Michaelis constant
=The Michaelis constant
![{\displaystyle {\ce {[S]}}}=](https://img.qammunity.org/2021/formulas/mathematics/middle-school/4gk32u0frnvq4e6zn9f2m58u125zi00j3e.png) Substrate concentration
Substrate concentration
(a) When
![[S]=30K_M](https://img.qammunity.org/2021/formulas/mathematics/middle-school/dn1ef0wg02o6xwxufhwsz31pcaxjlr2tei.png)
![(v)/(V_(max))=([S])/(K_M + [S])\\(v)/(V_(max))=(30K_M)/(K_M + 30K_M)\\(v)/(V_(max))=(30)/(1 + 30)\\(v)/(V_(max))=(30)/(31)\\$Expressed as a percentage\\(v)/(V_(max))=(30)/(31)X100=96.77\%](https://img.qammunity.org/2021/formulas/mathematics/middle-school/juo62i9cafwqz6xl6yxr1tjlzrk4eeecab.png)
(b)When
![K_M=30[S]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/t5vvnzsffdl3uodby3tginljb7vrwm2lat.png)
![(v)/(V_(max))=([S])/(K_M + [S])\\(v)/(V_(max))=([S])/(30[S] + [S])\\\\=(1[S])/(30[S] + 1[S])\\=(1)/(30 + 1)\\(v)/(V_(max))=(1)/(31)\\$Expressed as a percentage\\(v)/(V_(max))=(1)/(31)X100=3.23\%](https://img.qammunity.org/2021/formulas/mathematics/middle-school/v5olqkzs1fswnacm889gek2unh7no7wgk0.png)