Question

A prior study determined the point estimate of the population proportion as 58% ( = 0.58). The analysts decide to conduct a second study on the same topic and would like its margin of error, E, to be 4% when its confidence level is 95% (z*-score of 1.96).

What is the minimum sample size that should be used so the estimate of will be within the required margin of error of the population proportion?

Answer 1

585

Explanation:

Answer 2

Minimum Sample size 'n' = 585

Explanation:

Explanation:-

Given Estimate of the population proportion as 58% ( = 0.58)

P = 0.58

Given margin of error, E, to be 4%

M.E = 4 % = 0.04

margin of error of the population proportion is determined by

`M.E = \frac{Z_{(\alpha )/(2) }√(p(1-p)) }{√(n) }`

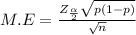
Z- score = 1.96

`0.04 = (1.96√(0.58(1-0.58)) )/(√(n) )`

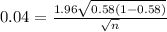
Cross multiplication , we get

`0.04 √(n) = 1.96 X 0.4935`

`√(n) = (0.4935 X 1.96)/(0.04) = 24.18`

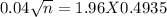
Squaring on both sides, we get

n = 584.7≅585

Conclusion:-

minimum Sample size 'n' = 585