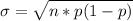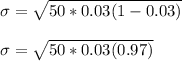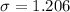Question

By one estimate, 3% of all Siberian Husky puppies are born with two different colored eyes (called

heterochromia iridum). For random samples of 50 Siberian Husky puppies, what are the mean and

standard deviation of the number of puppies that will have two different colored eyes?

(A) � = 0.03, � = 0.024

(B) � = 0.03, � = 0.171

(C) � = 1.5, � = 1.206

(D) � = 1.5, � = 1.455

(E) � = 3, � = 50

Answer 1

The population mean of the Siberian Husky puppies is
`\mathbf{ \mu = 1.5}`

The standard deviation of the Siberian Husky puppies is
`\sigma = 1.206`

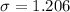
Explanation:

Given that:

3% of all Siberian Husky puppies are born with two different colored eyes

sample.

The population mean of the Siberian Husky puppies is:

`\mathbf{ \mu =( \sum x_i)/(N)}`

`\mathbf{ \mu =( (3)/(100))/(50)}`

`\mathbf{ \mu = (3)/(100)*{50}}`

`\mathbf{ \mu = 1.5}`

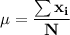
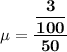
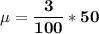
Standard deviation of Binomial experiment is calculated as:

`\sigma = √(n*p(1-p))`

`\sigma = √(50*0.03(1-0.03)) \\ \\ \sigma = √(50*0.03(0.97))`

`\sigma = 1.206`