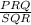Answer:
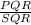
Explanation:
An isosceles triangle has two equal sides and the two opposite angles to the sides to be equal.
Given that; RP = RS, RQ and PS are common,
RP = SQ (opposite sides of parallelogram RPQS)
PQ = RS (opposite sides of parallelogram RPQS)
ΔRPS = ΔQPS (congruence property)
Thus comparing triangles PQR and SQR,
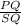 =
=
 (similarity property)
(similarity property)
<PRS = <PRQ + <SRQ (bisection of included <PRS)
<PQS = <PQR + <SQR (similatity property to <PRS)
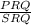 =
=
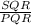 (congruence property)
(congruence property)
But, SRQ = PQR
So that;
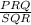
Therefore by Side-Angle-Side (SAS), the required additional fact is: