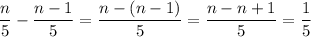Question

I have a basic exponential division question that I am pretty sure my Pearson is incorrect about.

7^n/5 / 7^n-1/5 SHOULD equal 1/7^1/5 BUT Pearson is saying the answer is 7^1/5.


Maybe I'm wrong. Help me out here. If you subtract n/5 -n-1/5 you should get -1/5, no?

edit: Oh wait... is it because 7^n/5 / 7^n-1/5 translates the denominator as a negative on top of the ruled negative?

aka 7^n/5 / 7^n-1/5 = n/5 - - n-1/5 ???

Answer 1

7^(n/5) / 7^((n -1)/5) = 7^(1/5)

Explanation:

First of all, you need parentheses on exponents that include any sort of arithmetic. You also need parentheses on any numerator or denominator that includes any sort of arithmetic. We assume you're interested in ...

7^(n/5) / 7^((n -1)/5)

Your subtraction needs to take into account the distributive property. The outside factor (-1) applies to every inside term.

`(n)/(5)-(n-1)/(5)=(n-(n-1))/(5)=(n-n+1)/(5)=(1)/(5)`