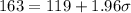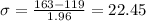Question

Use the following information to determine your answer: The length of a movie falls on a normal distribution. About 95% of movies fall between 75 minutes and 163 minutes.

What is the value of the standard deviation for average movie length in minutes? Please round to the second decimal place.

Answer 1

`75= 119 -1.96 \sigma`

`\sigma = (75-119)/(-1.96)= 22.45`

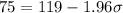
And tha's equivalent to use this formula:

`163= 119 +1.96 \sigma`

`\sigma = (163-119)/(1.96)= 22.45`

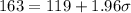
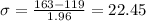
Explanation:

For this case the 95%of the values are between the following two values:

(75 , 163)

And for this case we know that the variable of interest X "length of a movie" follows a normal distribution:

`X \sim N( \mu, \sigma)`

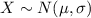
We can estimate the true mean with the following formula:

`\mu = (75+163)/(2)= 119`

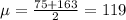
Now we know that in the normal standard distribution we know that we have 95% of the values between 1.96 deviations from the mean. We can find the value of the deviation with this formula:

`75= 119 -1.96 \sigma`

`\sigma = (75-119)/(-1.96)= 22.45`

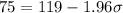
And tha's equivalent to use this formula:

`163= 119 +1.96 \sigma`

`\sigma = (163-119)/(1.96)= 22.45`