Answer:
There are 3,921,225 ways to select the winners.
Explanation:
This problem is about combinations with no repetitions, because the same person can't win four times. It's a combinaction because the order of winning doesn't really matter.
Combinations without repetitions are defined as

Where
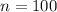 and
and
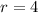 .
.
Replacing values, we have

Therefore, there are 3,921,225 ways to select the winners.
Additionally, as you can imagine, the probability of winning is extremely low, it would be 3,921,225 to 1.